Dave's Math Tables: Derivative x^n

(Math | Calculus | Derivatives | Table Of | x^n)

x^n = n x^(n-1)

3 Proofs

Proof of x^{^n} : from e^{^(n ln x)}

Given: e^{^x} = e^{^x}; ln(x) = 1/x; Chain Rule.
Solve:

x^{^n} = e^{^(n ln x)}

= e^{^u} (n ln x) (Set u = n ln x)

= [e^{^(n ln x)}] [n/x] = x^{^n} n/x = n x^{^(n-1)}     Q.E.D.

Proof of x^{^n} : from the Integral

Given: 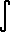x^{^n} dx = x^{^(n+1)}/(n+1) + c; Fundamental Theorem of Calculus.
Solve:

x^{^(n-1)} dx = x^{^n} / n

x^{^n} / n = x^{^(n-1)} dx = x^{^(n-1)}

1/n x^{^n} = x^{^(n-1)}

x^{^n} = n x^{^(n-1)}     Q.E.D.

Proof of x^{^n} : algebraicaly

Given: (a+b)^{^n} = (n, 0) a^{^n} b^{^0} + (n, 1) a^{^(n-1)} b^{^1} + (n, 2) a^{^(n-2)} b^{^2} + .. + (n, n) a^{^0} b^{^n}
Here (n,k) is the binary coefficient = n! / ( k! (n-k)! )

Solve:

x^{^n} = lim_(d->0) ((x+d)^{^n} - x^{^n})/d

= lim [ x^{^n} + (n, 1) x^{^(n-1)} d + (n, 2) x^{^(n-2)} d^{^2} + .. + x^{^0} d^{^n} - x^{^n} ] / d

= lim [ (n,1) x^{^(n-1)} d + (n, 2) x^{^(n-2)} d^{^2} + .. + x^{^0} d^{^n} ] / d

= lim (n,1) x^{^(n-1)} + (n, 2) x^{^(n-2)} d + (n, 3) x^{^(n-3)} d^{^2} + .. + x^{^0} d^{^n}

= lim (n, 1) x^{^(n-1)} (all terms on right cancel out because of the d factor)

= lim (n, 1) x^{^(n-1)} = n! / ( 1! (n-1)! ) x^{^(n-1)} = n x^{^(n-1)}     Q.E.D.